Calculer la Suite de Fibonacci, en s'aidant des tests, à la mode 3T, en 5 minutes

Date de publication : TODO.
Par
Thierry Leriche-Dessirier
Ce petit tutoriel montre comment mettre en oeuvre 3T (Tests en Trois Temps), pour développer une
fonctionnalité simple (la Suite de Fibonacci dans l'exemple) en s'aidant des tests, le tout
en quelques minutes.
1. Introduction
1-A. À propos
1-B. Avant de commencer
2. Découverte du projet d'exemple
2-A. Télécharger, installer et importer le projet d'exemple
2-B. Ce que fait déjà le projet
3. Action
3-A. Ajout d'un élément dans l'interface
3-B. Ajout des tests
3-C. Développement de la fonctionnalité
4. Conclusions
5. Remerciements
6. Annexes
6-A. Liens
6-B. Les fichiers importants en entier
6-C. Calculs alternatifs
6-C-1. Calcul direct
6-C-2. La solution de l'étudiant
6-D. Rapports finaux
6-E. Pour s'amuser
1. Introduction
3T (Tests en Trois Temps) est une déclinaison simplifiée et cadrée des TDD (Test Driven Developpement). Dans ce
petit tutoriel, nous allons l'utiliser et voir comment cette méthodologie peut nous aider à développer
une fonctionnalité.
Dans cet article, nous allons nous intéresser à la célèbre "Suite de Fibonacci" dont les premiers éléments
sont "1, 1, 2, 3, 5, 8, 13..." et dont le calcul est relativement simple. Ce choix nous dispensera d'avoir
à développer des algorithmes complexes qui nous détourneraient du sujet principal : les tests.
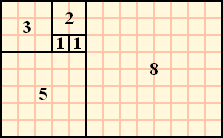
Carrés de Fibonacci en spirale
 |
La suite de Fibonacci, bien que simple en apparence, possède de nombreuses applications pratiques. La nature est
d'ailleurs intimement liée à cette série dont elle semble vouloir d'inspirer. On connait l'exemple des pommes
de pain et des tournesols. Les photographes savent en particulier que le rapport de deux membres consécutifs de
la suite de Fibonacci tend vers le fabuleux nombre d'or.
|
1-A. À propos
Découvrir une technologie n'est pas chose facile. En aborder plusieurs d'un
coup l'est encore moins. Partant de ce constat, cet article a été écrit pour aller à l'essentiel.
Les points importants sont présentés dans le corps de l'article et les
éléments secondaires sont expliqués en annexe.
1-B. Avant de commencer
Pour écrire ce tutoriel, j'ai utilisé les éléments suivants :
- Java JDK 1.6.0_24-b07 ;
- Eclipse Indigo 3.7 JEE 64b ;
- Maven 3.0.3 ;
- JUnit 4.8.2 ;
2. Découverte du projet d'exemple
2-A. Télécharger, installer et importer le projet d'exemple
 |
Pour suivre ce tutoriel, vous pouvez vous contenter de lire les codes
proposés ci-dessous (codes complets en annexe)
et de vous reperer à l'aide des captures d'écran.
|
2-B. Ce que fait déjà le projet
Le projet est relativement vide. Il n'y a aucune classe. Seul le fichier "pom.xml" contient
la configuration nécessaire pour utiliser des plugins de reporting.
Pour lancer la génération des différents rapports, il suffit d'executer la commande Maven suivante.
Cette commande va créer le dossier "target/site" avec en particulier le fichier "index.html" qui sert
de page d'accueil pour consulter les rapports. Sans surprise, puisque le projet est initialement "vide",
le reporting est relativement vide également.
3. Action
Nous allons voir comment utiliser "3T" pour développer la fonctionnalité "024", définit (page 45) dans le
cahier des charges (fictif), et correspondant au calcul des éléments de la Suite de Fibonacci.
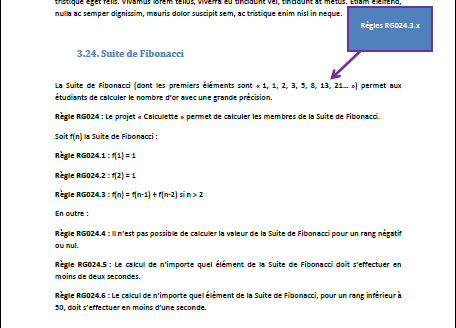
Page 45 du cahier des charges (cliquer pour voir la page en entier)
 |
Le PDF de la page 45 du cahier des charges (fictif) est disponible dans le Zip du projet d'exemple.
|
3-A. Ajout d'un élément dans l'interface
Durée estimée : 1 minute.
 |
Dans ce tutoriel, nous allons considérer que la Suite de Fibonacci est la première qu'on
développe, et qu'il n'y a donc aucun code pré-existent.
|
On commence donc par créer l'interface "Calculette.java" dans laquelle on spécifie ce que doit
faire la fonctionnalité. C'est la première étape définie par 3T.
| Calculette.java |
public interface Calculette {
Long fibonacci(Integer n);
}
|
Conformément aux préconisations de 3T, on ajoute un peu de documentation. Pour cela, on se contente
de recopier le cahier des charges.
| Calculette.java |
public interface Calculette {
@param
@return
Long fibonacci(Integer n);
}
|
Les développeurs ont identifié des règles implicites dans le cahier des charges. Ces règles ont
été indiquées à l'aide du réctangle bleu, avec la référence "RG024.3.x". Puisqu'on a la chance d'avoir
de nombreux exemples, on les ajoute à la documentation.
| Calculette.java |
public interface Calculette {
@param
@return
Long fibonacci(Integer n);
}
|
On peut dès à présent lancer la génération des rapports. Le plugin "taglist", en particulier,
nous indique la liste de toutes les règles que nous allons prendre en compte. Cette information
est utile pour tous les membres de l'équipe, en particulier pour le chef de projet.
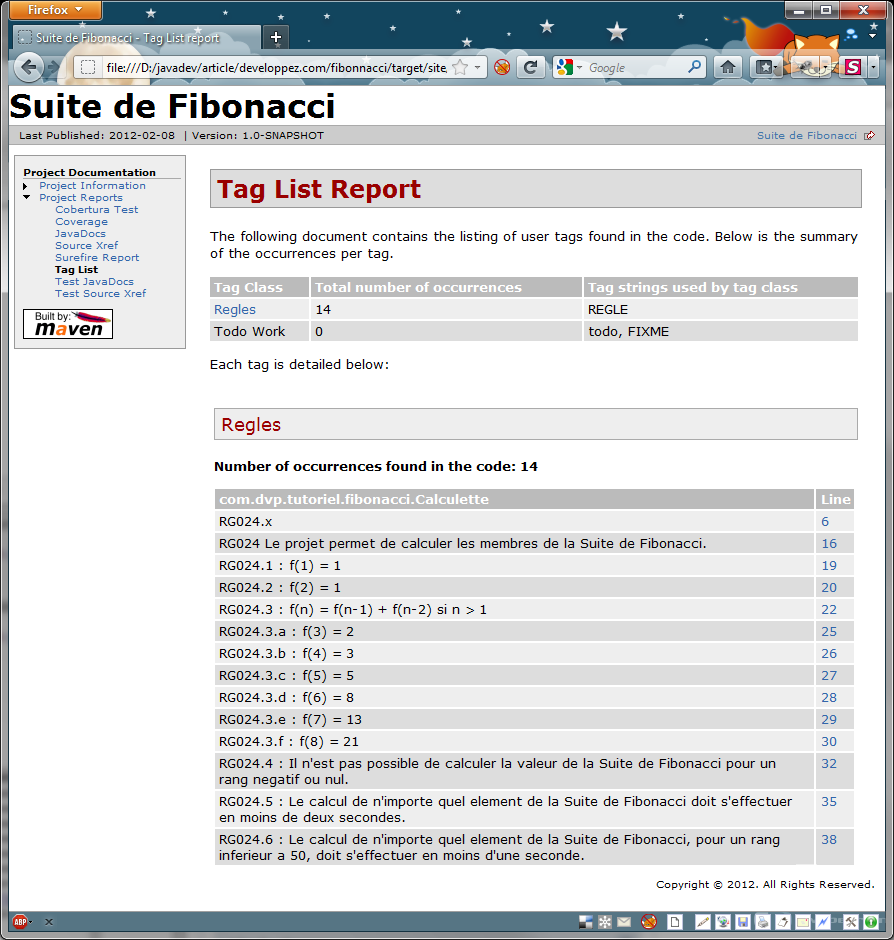
Règles prises en compte.
Pour finir cette étape, on crée l'implémentation "MaCalculette" déstinée à recevoir le code, en la laissant vide.
| MaCalculette.java |
public class MaCalculette implements Calculette {
@Override
public Long fibonacci(Integer n) {
throw new UnsupportedOperationException("Cette fonction n'est pas encore disponibles.");
}
}
|
3-B. Ajout des tests
Durée estimée : 3 minutes.
 |
3T conseille que le développeur qui code les tests ne soit pas celui qui a déjà écrit l'interface.
|
On ne code pas directement la fonctionnalité. On écrit d'abord des tests. Pour cela, on s'inspire
de l'interface qu'on vient de créer.
C'est la deuxième étape définie par 3T.
| MaCalculetteTest.java |
public class MaCalculetteTest {
private Calculette calculette;
@Before
public void doBefore() {
calculette = new MaCalculette();
}
@Test
public void testBidon() {
Assert.assertFalse(1 == 2);
}
}
|
 |
Par habitude, je commence toujours par créer un test "bidon" pour vérifier que JUnit
fonctionne correctement. Je supprime ce test immédiatement après avoir constaté que tout va bien,
pour ne pas polluer le code.
|
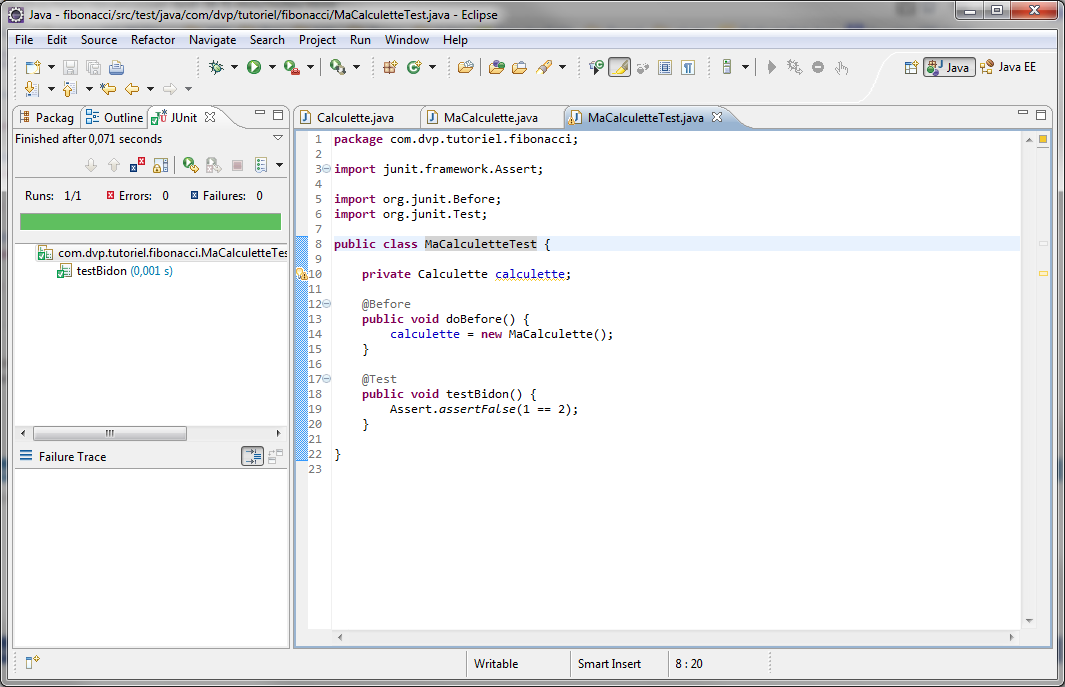
JUnit dans Eclipse
On écrit ensuite les tests. Conformément à 3T, on écrit un test (dédié) pour chaque règle.
| MaCalculetteTest.java |
@Test
public void testFibonacci_RG024_1() {
final Integer n = 1;
final Integer resultatAttendu = new Long(1);
final Long resultatCalcule = calculette.fibonacci(n);
Assert.assertEquals(resultatAttendu, resultatCalcule);
}
|
Conformément à 3T, on utilise le formalisme AAA (Arrange, Act, Assert) pour organiser les tests
et rendre la lecture plus simple. On écrit aussi un peu de documentation en recopiant le numéro
de la règle testée et en précisant les paramètre envoyés et la réponse attendue.
Quand on lance le test, il doit être rouge dans Eclipse, ce qui est logique puisque la fonctionnalité
n'est pas encore programmée.
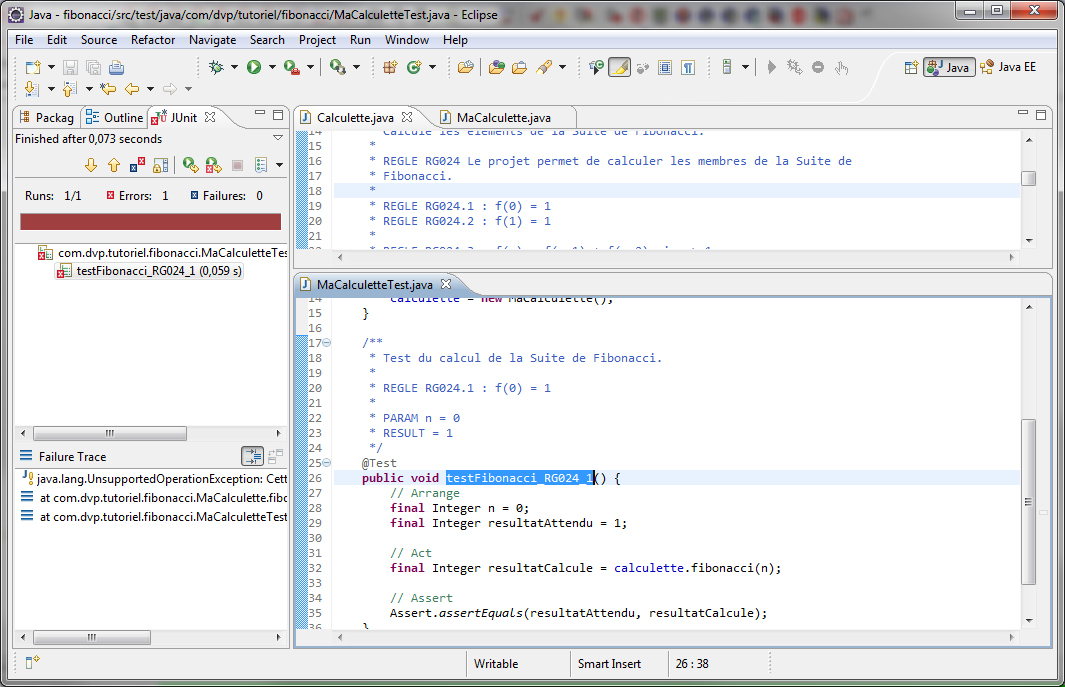
Le(s) test(s) est rouge
On fait de même pour l'ensemble des règles, en factorisant ce qui peut l'être.
| MaCalculetteTest.java |
public class MaCalculetteTest {
private Calculette calculette;
@Before
public void doBefore() {
calculette = new MaCalculette();
}
@Test
public void testFibonacci_RG024_1() {
final Integer n = 1;
final long resultatAttendu = 1;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_2() {
final Integer n = 2;
final long resultatAttendu = 1;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_a() {
final Integer n = 3;
final long resultatAttendu = 2;
testFibonacci_RG024_x(n, resultatAttendu);
}
...
@Test(expected = IllegalArgumentException.class)
public void testFibonacci_RG024_4_a() {
final Integer n = 0;
testFibonacci_RG024_x(n, null);
}
...
@Test(timeout = 2000)
public void testFibonacci_RG024_5() {
final Integer n = 55;
final long resultatAttendu = 139583862445L;
testFibonacci_RG024_x(n, resultatAttendu);
}
...
private void testFibonacci_RG024_x(Integer n, Long resultatAttendu) {
final Long resultatCalcule = calculette.fibonacci(n);
assertEquals(resultatAttendu, resultatCalcule);
}
}
|
Conformément aux TDD, tous les tests doivent être rouges à ce stade.
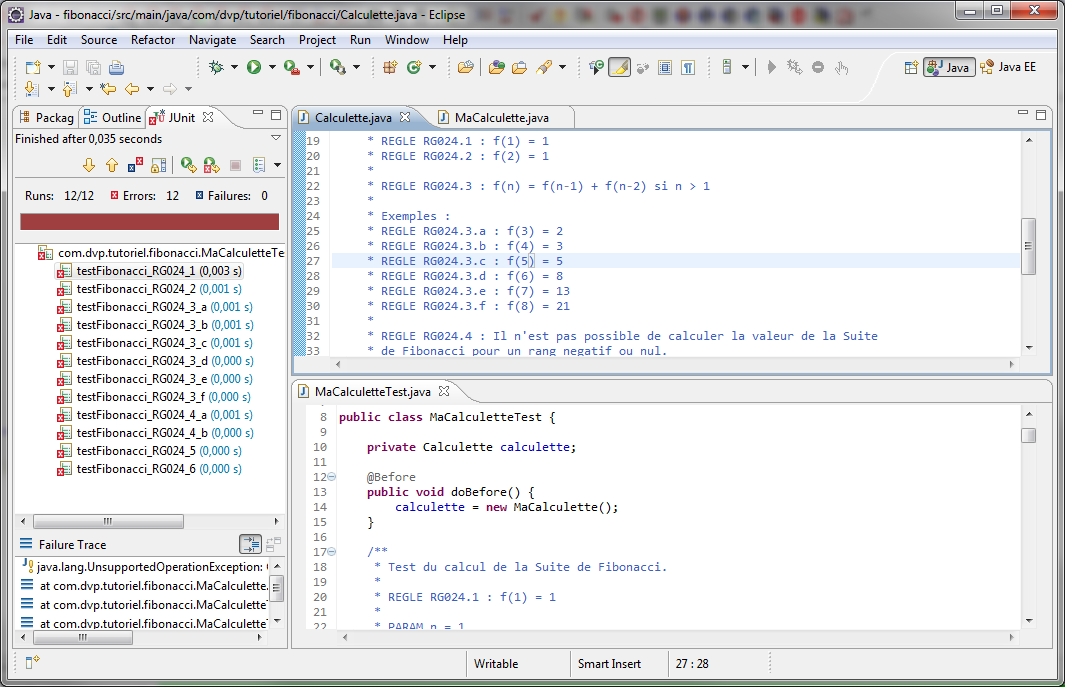
Tous les tests sont rouges
On peut à nouveau demander à Maven de générer les reporting. Le rapport Surefire, en particulier, montre
que tous les tests échouent.
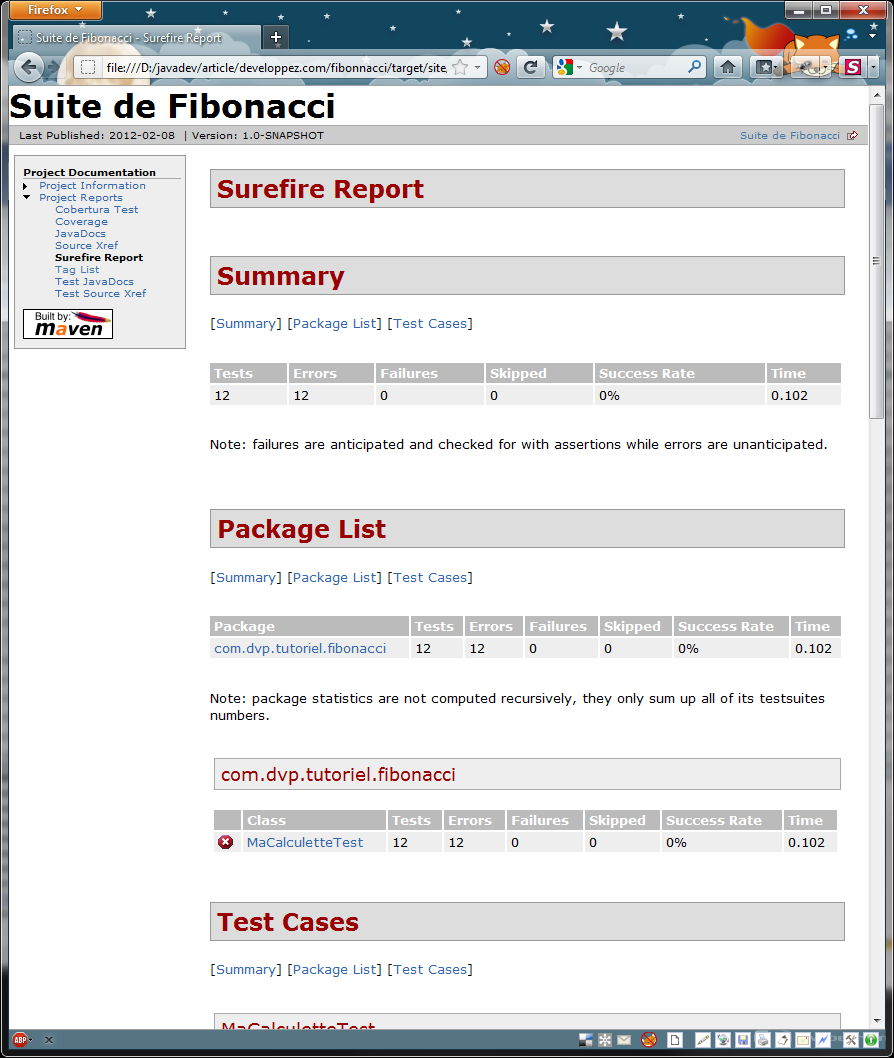
Tous les tests sont en échec
Le chef de projet peut utiliser ce rapport pour suivre l'avancée des développements.
3-C. Développement de la fonctionnalité
Durée estimée : 2 minute.
Maintenant que l'interface et les tests sont écrits, on peut programmer la fonctionnalité à proprement
parlé. C'est la troisième et dernière étape définie par 3T. Lorsque tous les tests seront verts, on pourra
légitimement penser que le code est terminé.
 |
3T conseille que le développeur qui programme la fonctionnalité ne soit pas celui qui a déjà codé les tests.
|
On peut programmer les règles dans l'ordre qu'on veut. Faute de mieux, on peut en particulier les prendre
dans l'ordre. Dans le code, on en profite pour rappeler les références des règles.
| MaCalculette.java |
public class MaCalculette implements Calculette {
@Override
public Long fibonacci(Integer n) {
if(n == 1) {
return 1L;
}
throw new UnsupportedOperationException("Cette fonction n'est pas encore disponibles.");
}
|
On relance les tests et on constate que le test lié à la règle "RG024.1" est bien passé au vert.
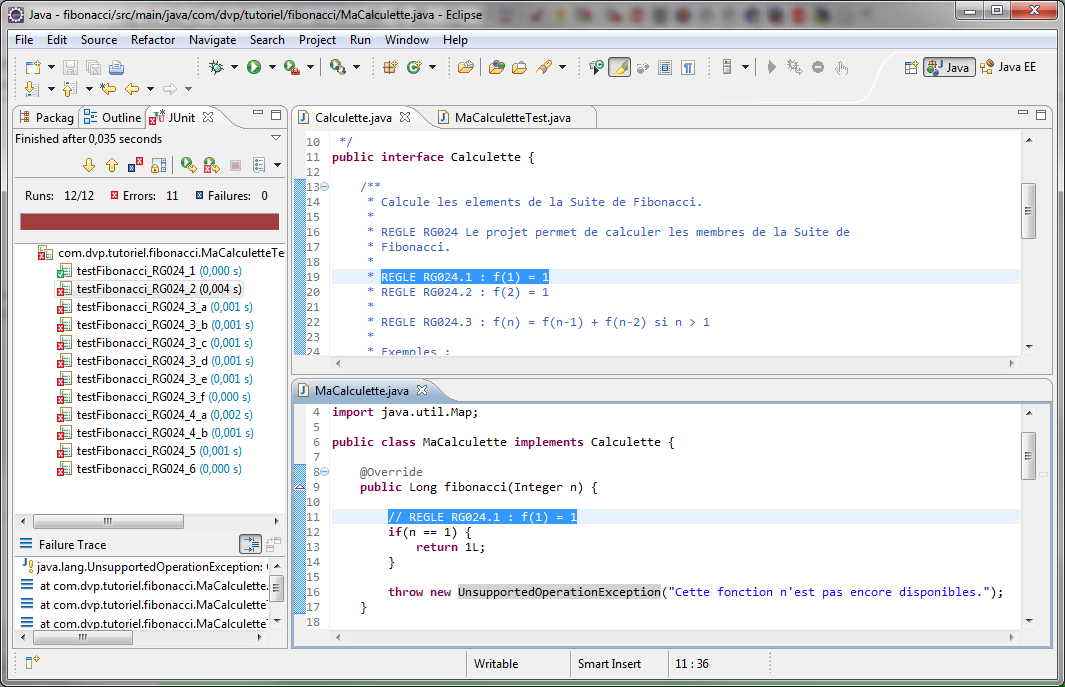
Le test de RG024.1 est vert
On continue avec la règle suivante.
| MaCalculette.java |
public class MaCalculette implements Calculette {
@Override
public Long fibonacci(Integer n) {
if(n == 1 || n == 2) {
return 1L;
}
throw new UnsupportedOperationException("Cette fonction n'est pas encore disponibles.");
}
|
On relance les tests et on constate que le test lié à la règle "RG024.2" est bien passé au vert.
 |
Au passage, on vérifie que les tests déjà verts restent bien verts. Si c'est le cas, on peut continuer
en mode automatique. Si, au contraire, un test précédement vert devient rouge, cela signifie qu'on
vient de créer une regression. Il faut alors poser le stylo et analyser ce qui ne va pas.
|
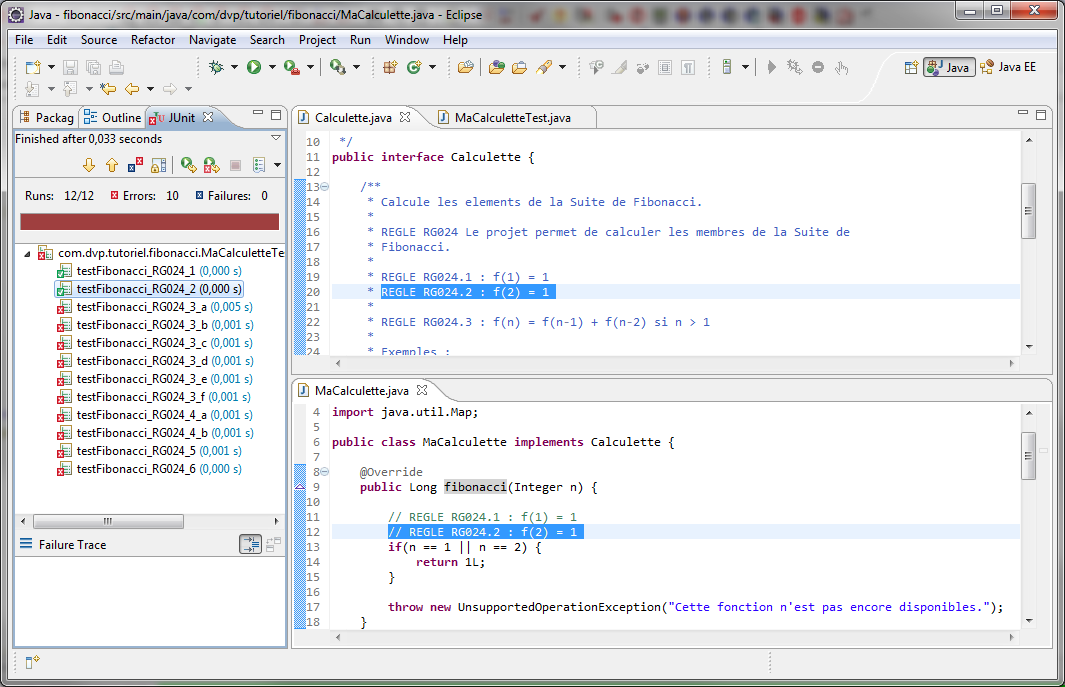
Le test de RG024.2 est vert
On continue avec la (les) règle(s) suivante(s).
| MaCalculette.java |
public class MaCalculette implements Calculette {
@Override
public Long fibonacci(Integer n) {
if(n == 1 || n == 2) {
return 1L;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
|
On relance les tests et on constate que de nouveaux tests sont passé au vert. On est donc sur le bon chemin.
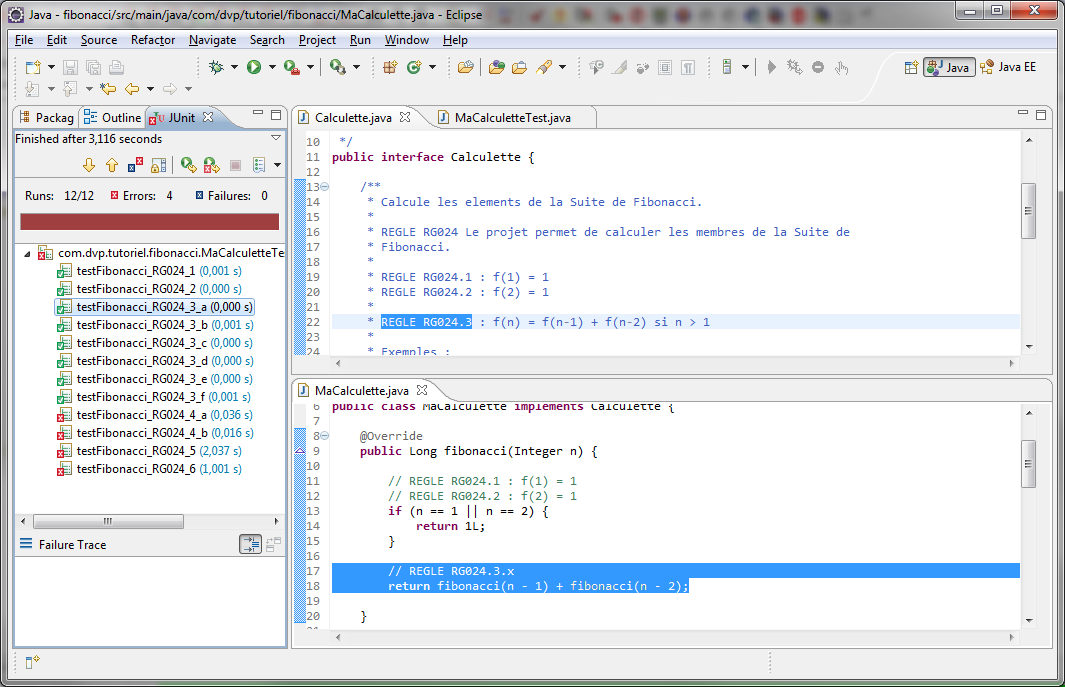
De nouveaux tests sont verts
On continue avec la (les) règle(s) suivante(s).
| MaCalculette.java |
public class MaCalculette implements Calculette {
@Override
public Long fibonacci(Integer n) {
if(n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
if(n == 1 || n == 2) {
return 1L;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
|
On relance les tests et on constate que de nouveaux tests sont passé au vert. On approche du but.
On continue avec les règles suivantes. Ce sont les premières qui vont demander un peu de reflexion.
| MaCalculette.java |
public class MaCalculette implements Calculette {
private static Map<Integer, Long> map = new HashMap<Integer, Long>();
@Override
public Long fibonacci(Integer n) {
if(n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
if (n == 1 || n == 2) {
return 1L;
}
Long valeur = map.get(n);
if (valeur != null) {
return valeur;
}
valeur = fibonacci(n - 1) + fibonacci(n - 2);
map.put(n, valeur);
return valeur;
}
}
|
On relance les tests et on constate que tous les tests sont désormais verts.
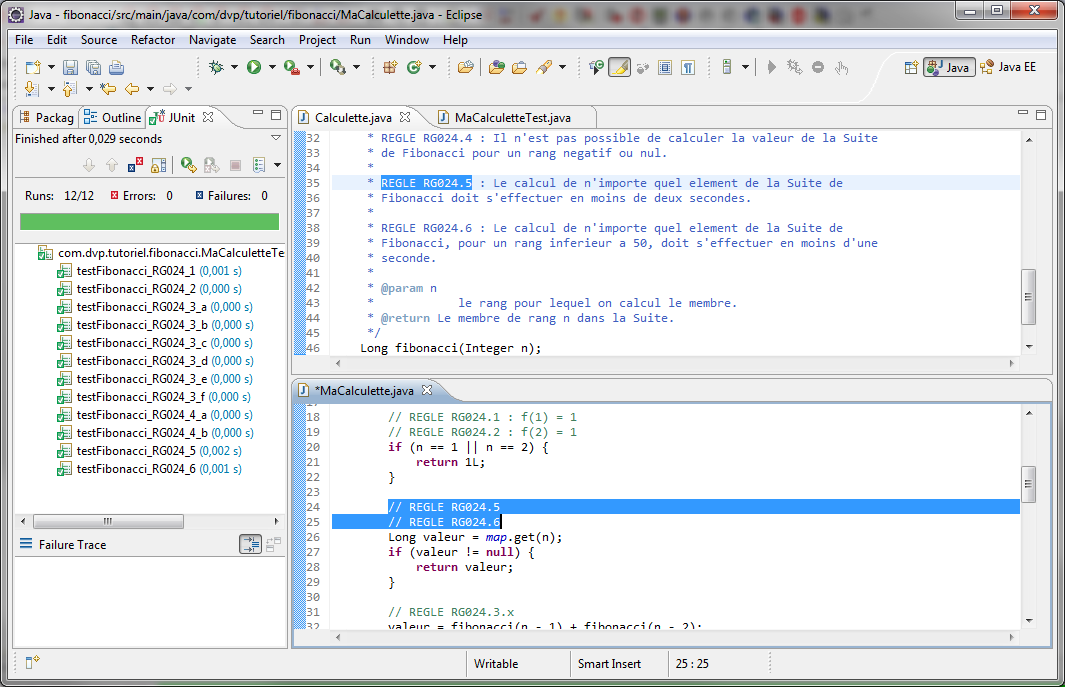
Tous les tests sont verts
Le rapport Surefire (JUnit), quant à lui, confirme que tous les tests passent avec succès, ce qui
devrait ravir le chef de projet.
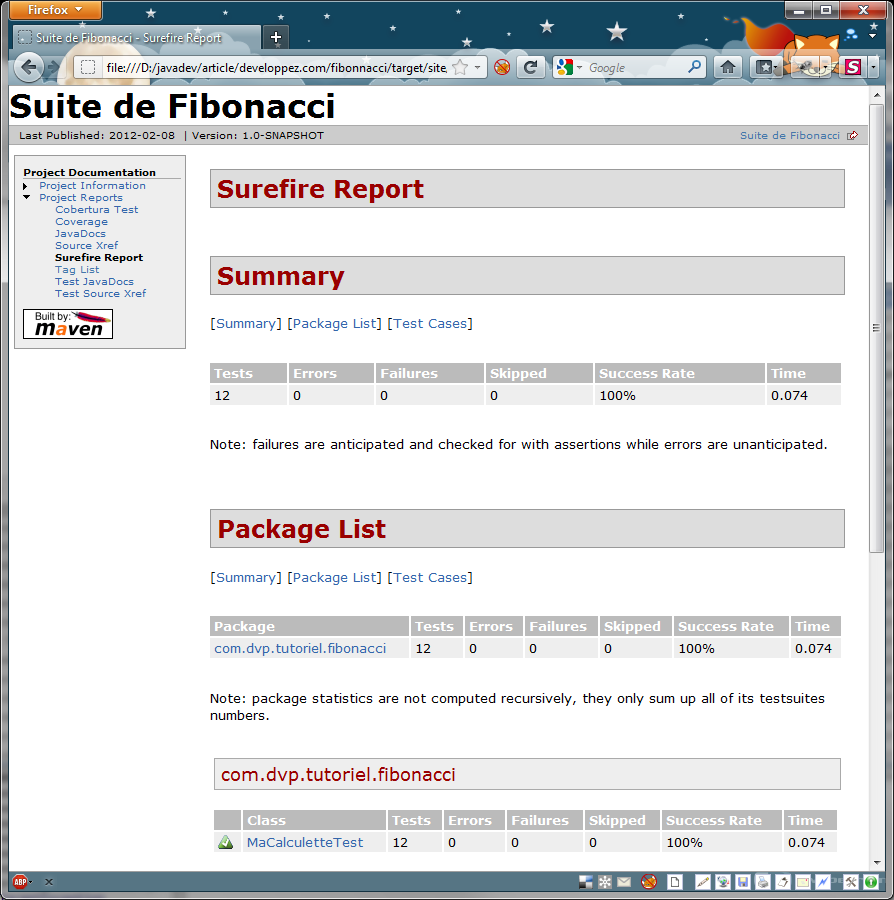
Surefire indique que tout est bon
Et voilà...
4. Conclusions
Comme on vient de le voir dans ce petit tutoriel, il est très simple d'écrire une fonctionnalité
en utilisant 3T (Tests en Trois Temps) car on est guidé tout du long. Le processus se déroule en
trois étapes : écriture de l'interface, écriture des tests puis développement de la fonction. Chaque
étape d'inspire largement sur la précédente. 3T conseille en outre que chaque étape soit réalisée par
une personne différente.
Pour écrire l'interface, il suffit de recopier le cahier des charges. Pour coder les tests, il suffit
de reprendre la documentation de l'interface et de la mettre en forme. Enfin, pour développer la fonctionnalité,
il suffit de se laisser guider par les tests, comme on le ferait avec les TDD (Test Driven Developpement).
La plupart du temps, cette démarche est quasi systèmatique, permettant aux développeurs de se concentrer
sur l'essentiel.
Le code final de ce tutoriel est disponible dans le fichier ZIP
fibo2.zip. Les rapports générés sont également disponibles dans le Zip, dans le
dossier "site".
Le fichier
fibo3.zip, quant à lui, contient également le code des solutions proposées en annexe,
et réorganisé pour prendre en compte plusieures solutions.
5. Remerciements
Je tiens à remercier, en tant qu'auteur de tutoriel
rapide, toutes les personnes qui m'ont aidé et soutenu. Je pense
tout d'abord à mes collègues qui subissent mes questions au
quotidien mais aussi à mes contacts et amis du Web, dans le domaine
de l'informatique ou non, qui m'ont fait part de leurs remarques et
critiques. Bien entendu, je n'oublie pas l'équipe de developpez.com
qui m'a guidé dans la rédaction de cet article et m'a aidé à le
corriger et le faire évoluer, principalement sur le forum.
6. Annexes
6-A. Liens
6-B. Les fichiers importants en entier
Par ordre de développement...
| Interface Calculette.java |
public interface Calculette {
@param
@return
Long fibonacci(Integer n);
}
|
| Tests MaCalculetteTest.java |
import static junit.framework.Assert.assertEquals;
import org.junit.Before;
import org.junit.Test;
@author
public class MaCalculetteTest {
private Calculette calculette;
@Before
public void doBefore() {
calculette = new MaCalculette();
}
@Test
public void testFibonacci_RG024_1() {
final Integer n = 1;
final long resultatAttendu = 1;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_2() {
final Integer n = 2;
final long resultatAttendu = 1;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_a() {
final Integer n = 3;
final long resultatAttendu = 2;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_b() {
final Integer n = 4;
final long resultatAttendu = 3;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_c() {
final Integer n = 5;
final long resultatAttendu = 5;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_d() {
final Integer n = 6;
final long resultatAttendu = 8;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_e() {
final Integer n = 7;
final long resultatAttendu = 13;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test
public void testFibonacci_RG024_3_f() {
final Integer n = 8;
final long resultatAttendu = 21;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test(expected = IllegalArgumentException.class)
public void testFibonacci_RG024_4_a() {
final Integer n = 0;
testFibonacci_RG024_x(n, null);
}
@Test(expected = IllegalArgumentException.class)
public void testFibonacci_RG024_4_b() {
final Integer n = -1;
testFibonacci_RG024_x(n, null);
}
@Test(timeout = 2000)
public void testFibonacci_RG024_5() {
final Integer n = 55;
final long resultatAttendu = 139583862445L;
testFibonacci_RG024_x(n, resultatAttendu);
}
@Test(timeout = 1000)
public void testFibonacci_RG024_6() {
final Integer n = 49;
final long resultatAttendu = 7778742049L;
testFibonacci_RG024_x(n, resultatAttendu);
}
private void testFibonacci_RG024_x(Integer n, Long resultatAttendu) {
final Long resultatCalcule = calculette.fibonacci(n);
assertEquals(resultatAttendu, resultatCalcule);
}
}
|
| Implémentation MaCalculette.java |
import java.util.HashMap;
import java.util.Map;
public class MaCalculette implements Calculette {
private static Map<Integer, Long> map = new HashMap<Integer, Long>();
@Override
public Long fibonacci(Integer n) {
if (n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
if (n == 1 || n == 2) {
return 1L;
}
Long valeur = map.get(n);
if (valeur != null) {
return valeur;
}
valeur = fibonacci(n - 1) + fibonacci(n - 2);
map.put(n, valeur);
return valeur;
}
}
|
Sans oublier le fichier "pom.xml"...
6-C. Calculs alternatifs
6-C-1. Calcul direct
Le calcul récursif est rarement le plus efficasse. A la place, je propose la méthode de calcul suivante,
faisant largement appel à mes vieux souvenir de math et, accessoirement, à Wikipedia.
| Implémentation MaCalculette2.java |
public class MaCalculette2 implements Calculette {
private final static double NOMBRE_OR = 1.61803398874989;
private final static double RACINE_5 = 2.236067977499;
@Override
public Long fibonacci(Integer n) {
if(n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
if (n == 1 || n == 2) {
return 1L;
}
final double nominateur = Math.pow(NOMBRE_OR, n);
final double result = nominateur / RACINE_5;
return Math.round(result);
}
|
 |
Cette méthode, bien que très rapide, ne fonctionne plus au delà d'un certain rang. Cela provient des
approximations numériques utilisées. Toutefois, selon le besoin (avoir rapidement une valeur ou avoir un
valeur exacte), elle peut s'avérer suffisante...
|
Bien entendu, il faut ajouter quelques tests pour valider cette version. On en profite pour
réorganiser un peu le code.
| Test (abstract) AbstractMaCalculetteTest.java |
public abstract class AbstractMaCalculetteTest {
protected static Calculette calculette;
@Test
public void testFibonacci_RG024_1() {
final Integer n = 1;
final long resultatAttendu = 1;
testFibonacci_RG024_x(n, resultatAttendu);
}
...
|
On adapte "MaCalculetteTest.java" en fonction et on crée "MaCalculette2Test.java"
dans la foulée.
| Test MaCalculetteTest.java remanié |
public class MaCalculetteTest extends AbstractMaCalculetteTest {
@Before
public void doBefore() {
calculette = new MaCalculette();
}
}
|
| Test MaCalculette2Test.java |
public class MaCalculette2Test extends AbstractMaCalculetteTest {
@Before
public void doBefore() {
calculette = new MaCalculette2();
}
@Test
public void testFibonacci_RG024_3_divergeance() {
final Integer n = 70;
final long resultatAttendu = 190392490709135L;
testFibonacci_RG024_x(n, resultatAttendu);
}
}
|
Le test "testFibonacci_RG024_3_divergeance" échoue, montrant que la précision des valeurs
utilisées n'est plus suffisante dès le rang "70";
6-C-2. La solution de l'étudiant
Quelques uns de mes étudiants prennent un racourçi qui n'est pas dénoué de sens, même s'il est en
général emprunté pour de mauvaises raisons.
| Implémentation MaCalculette3.java |
public class MaCalculette3 implements Calculette {
@Override
public Long fibonacci(Integer n) {
if (n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
switch (n) {
case 1:
case 2:
return 1L;
case 3: return 2L;
case 4: return 3L;
case 5: return 5L;
case 6: return 8L;
case 7: return 13L;
case 8: return 21L;
default:
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
}
|
Ce n'est pas génial mais c'est hyper rapide pour les éléments pris en compte. Comme
les professeurs ne vérifient généralement que les premières valeurs, les élèves s'en tirent
à bon compte, et avec de très bonnes performances. Ce code échoue néanmoins lors du test
des règles "RG024.5" et "RG024.6" avec des valeurs de "n" plus importantes.
On peut toutefois s'en inspirer en combinant des valeurs pré calculées, et stockées dans un fichier
CSV par exemple, avec une map comme proposé plus haut.
| Implémentation MaCalculette4.java |
public class MaCalculette4 implements Calculette {
private static Map<Integer, Long> map;
private static MaCalculette4 instance = new MaCalculette4();
private MaCalculette4 () {
FibonacciDao dao = new FibonacciDao();
map = dao.charger();
}
public static synchronized MaCalculette4 getInstance() {
return instance;
}
@Override
public Long fibonacci(Integer n) {
if (n <= 0) {
throw new IllegalArgumentException("On ne calcule que pour des nombres positifs");
}
if (n == 1 || n == 2) {
return 1L;
}
Long valeur = map.get(n);
if (valeur != null) {
return valeur;
}
valeur = fibonacci(n - 1) + fibonacci(n - 2);
map.put(n, valeur);
return valeur;
}
}
|
Le fichier "fibonacci.csv" ressemblerait alors au code suivant.
| fibonacci.csv |
# Suite de Fibonacci
Rang,membre
1,1
2,1
3,2
4,3
5,5
6,8
7,13
8,21
9,34
10,55
11,89
12,144
13,233
14,377
15,610
16,987
17,1597
18,2584
19,4181
20,6765
21,10946
22,17711
23,28657
24,46368
25,75025
26,121393
27,196418
28,317811
29,514229
30,832040
...
|
Je crée, bien entendu, une classe de test pour vérifier que tout est bon, en suivant les recommandations
de 3T.
| Test MaCalculette4Test.java |
public class MaCalculetteTest4 extends AbstractMaCalculetteTest {
@BeforeClass
public static void doBeforeClass() {
calculette = MaCalculette4.getInstance();
}
}
|
6-D. Rapports finaux
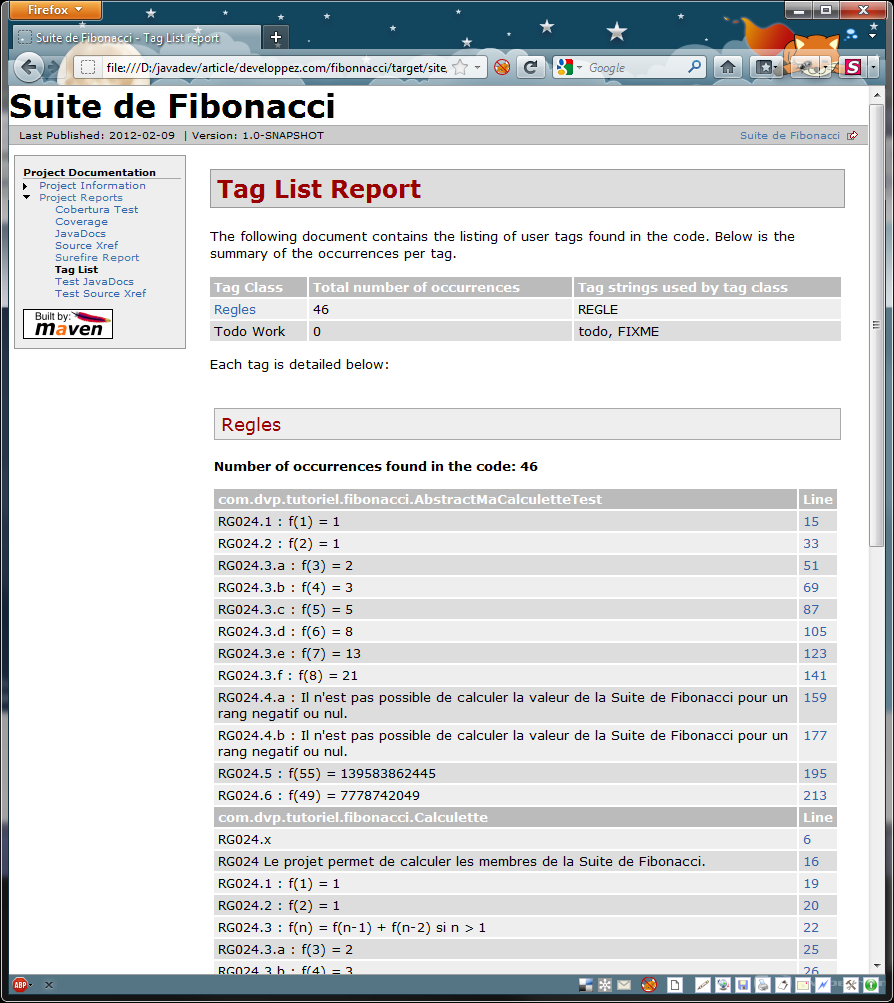
Liste des règles (taglist) dans le code
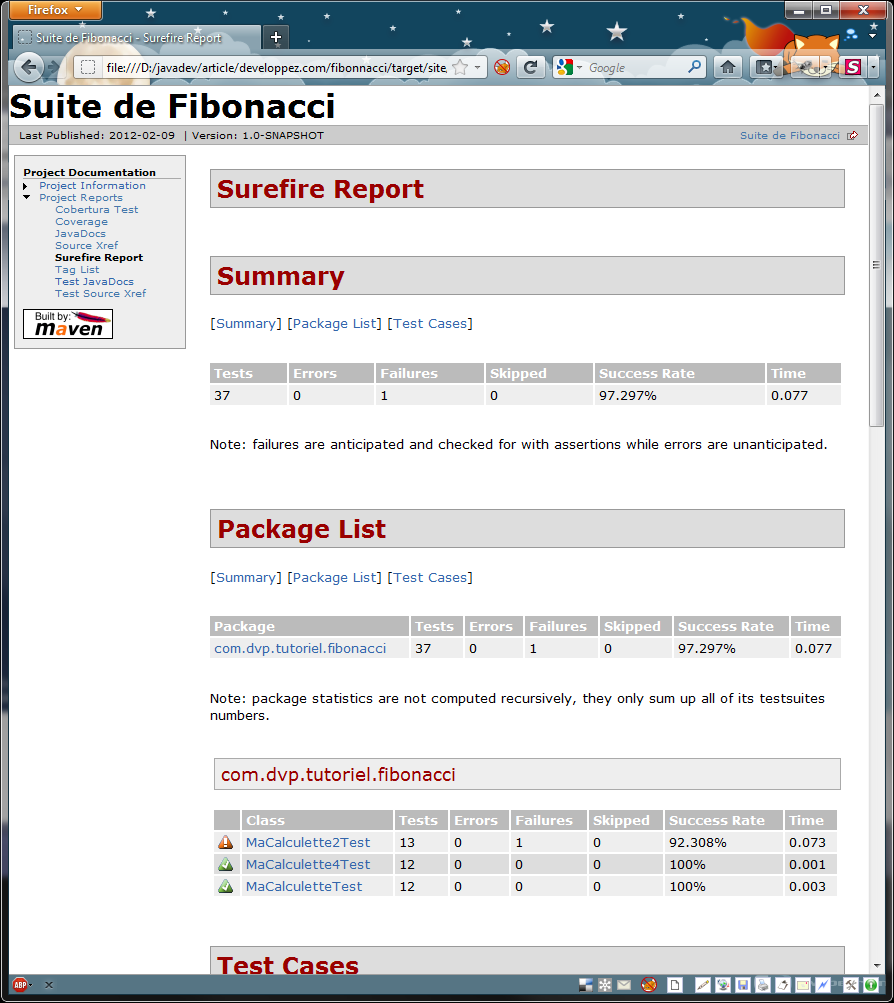
Rapport Surefire
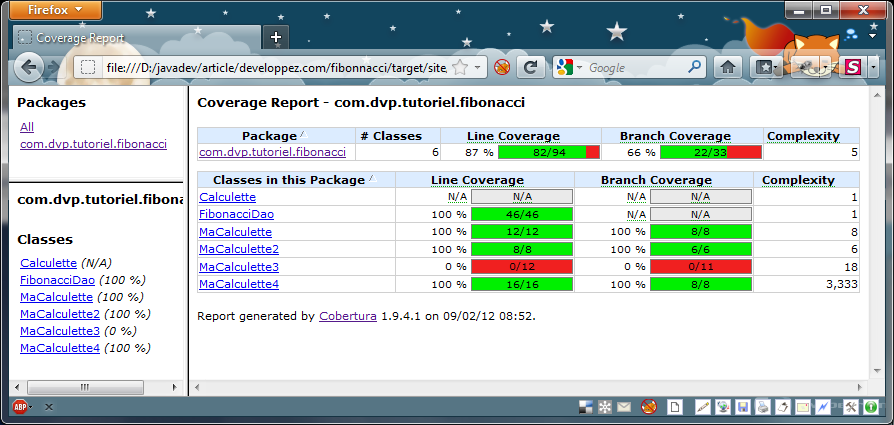
Couverture de test avec Cobertura
6-E. Pour s'amuser
Pour aller plus loin et/ou s'entrainer, on peut aussi développer, sur le même modèle (3T),
les Suites de Lucas et les Suites de k-bonacci.


Les sources présentées sur cette page sont libres de droits
et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation
constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright ©
2011 Thierry Leriche-Dessirier. Aucune reproduction, même partielle, ne peut être
faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.

























